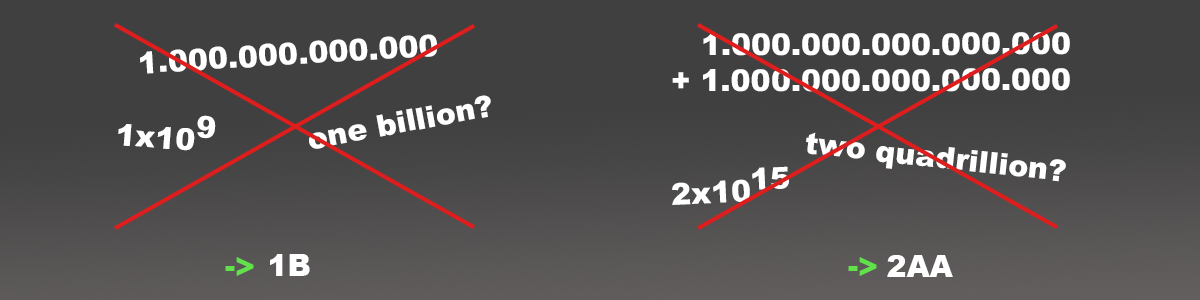If you ever played idle games before, you surely noticed how fast numbers in these games grow, even after only playing for a short amount of time. This exponential growth poses some challenges for developers though.
Usually, games just use primitive numeric data types, but those are limited (varies depending on the language / platform). In our environment (Unity, C#), the numeric data type that can hold the biggest range of numbers is double with a scale from ±5×10-324 to ±1.7×10308. This seems huge and most games will never reach these limits. But with idle games, it’s different:
Some idle games are getting away with just using primitive numeric data types and deal with it incorporating this drawback into the game design by resetting currencies or even the whole game state after certain milestones. Alternatively, introducing new higher value currencies (silver → gold) can also be a solution, once limits are reached. This would mean storing each currency in its own variable and converting currencies back and forth between them. Once a currency becomes irrelevant, it can be abandoned/deleted.
But how do you deal with it when the premise is a persistence layer that will have a global currency and will not be replaced. There won’t be any resets – we’ll use it from the beginning to the end.
Another solution is needed!
To solve this challenge, the first task was to check out existing implementations for large numbers, so I looked into numeric data types like BigInt and BigFloat which can hold arbitrary large numbers.
After playing around with them and trying out operations on values that we are very likely to reach, I noticed how slow these operations were (at least 50x slower compared to Int64 but, depending on size and operation, significantly worse).
There might also be a size issue which can occur once the numbers are big enough. This could potentially affect memory and also transmission of these numbers through the network. So I realized, as easy as working with them is, they are not a suitable solution for us. Additionally they are immutable, so each operation on them will create a new instance, amplifying some of the before mentioned issues.
I did some more research on other idle games and while doing so, stumbled over a custom idle number implementation that looked promising idle-bignum. It is very small and easy to understand so I quickly ported it to C# (from now on referred as IdleNumber) and tested it out. With some adjustments, it meets our requirements and it is fast enough. The implementation is semi-immutable though: depending on the operation new instances will get created.
| Operation (10k iterations) | float | IdleNumber | BigFloat |
| + | 1ms | 9ms | 142ms |
| – | 0ms | 8ms | 128ms |
| * | 0ms | 4ms | 74ms |
| / | 1ms | 9ms | 93ms |
Of course, with achieving this speed advantage there are also downsides:
- We have a maximum value an IdleNumber can hold as it internally consists of a double (64 bit) and an (u)int (32 bit)
- The double value has a precision of ( ~15-17 digits), which could result in precision loss and thus inaccurate numbers
But these limitations are fine with us:
- The number it can hold is far bigger as what we anticipate to ever display in the game (a 4,294,967,298 digit number)
- At some point the precision loss will start to affect lower digits of our IdleNumber. These should become insignificant to the player anyway. Besides that it is not a problem exclusive to this implementation. I will explain what this means for us later in “When does precision loss happen?“
So how does the system work?
An IdleNumber stores two values (all code snippets following are written in pseudo code):
double Value; (u)int Exp;
With it, we can (optionally) use a range of up to 9007199254740991L (biggest integer value we can store precisely as a double) for Value without precision loss. Exp, the exponent, indicates the amount of digits the decimal point is shifted:
new IdleNumber(12, 3); > 12000
Aligning numbers
Idle numbers with differing exponents need to be aligned when we do mathematical operations on them. We always need to align them to the bigger Exp as it represents a higher significance.
IdleNumber smallExp = new IdleNumber(234, 2); IdleNumber bigExp = new IdleNumber(999.45, 4); int diff = bigExp.Exp - smallExp.Exp; > 2 smallExp.Value = smallExp.Value / Math.Pow(10, diff); > 2.34 smallExp.Exp > 4
Performing mathematical operations
Once the numbers are aligned, we can easily perform operations on them. For additions we just need to add both Values (taking bigExp and smallExp from the previous example).
IdleNumber result = smallExp + bigExp; result.Value; > 1002.79 result.Exp; > 4
Normalizing the number
You may have noticed that Value of result has 4 pre-decimal point digits now. This means the number already falls into the next bigger unit bracket and needs to be aligned to a higher Exp.
To achieve this, we normalize the number. Normalizing can happen in two directions: some operations may result in a number >= 1000, some in numbers <1.
So what we have to do in our example is to loop through the Value as long as it is >=1000 and in every loop, divide it by 1000 and add 3 (3 additional digits) to the Exp:
while (Math.Abs(Value) >= TenCubed)
{
Value /= TenCubed;
Exp += 3;
}
Afterwards our number looks like this:
result.Value; > 1.00279 result.Exp; > 7
When does precision loss happen?
In the step before, you noticed how our decimal point moved a few digits. Let’s add a huge number and see what happens:
IdleNumber bigExp = new IdleNumber(1.00279 , 7); IdleNumber hugeExp = new IdleNumber(1, 17); IdleNumber result = bigExp + hugeExp; result.Value; > 1.00000000010028 result.Exp; > 17
You can see that our number is not accurate anymore as Value should be 1.000000000100279 and is now represented as 1.00000000010028.
But why does this happen?
Going into detail about floating-point arithmetic opens a whole new can of worms. To keep it short, let’s leave it at this:
Double representation is finite. So not all the real numbers can be precisely represented. In C# the precision is 15 digits for double values and unfortunately, by normalizing our number we just reached that limit with our Value of 1.00000000010028. This is the first time we lose precision.
You can find out more about how floating point precision works here.
Does it matter?
There are ways avoiding precision loss, but it doesn’t really matter for us, as long as operations are fast and the imprecision is neglectable. If we print the number it reads 100,000,000,010,028,000 (100 Quadrillion) with an imprecision of 1000 – a difference the player shouldn’t care about and will not even see (as we only show two decimals, see next point).
Fun fact: In our first implementation of IdleNumber was mutable. After doing an operation where the Exps where largely different it sometimes happened that, due to the aligning, a number is now more imprecise than before. In the worst case it would just be zero. That may have been alright for that operation, but due to it’s mutability all following operations will continue using this new number, causing improper results.
Formatting the number
You could use the scientific notation (1e1, 1e2, 1e3) or engineering notation (1e0, 1e3, 1e6) to display the idle number but after talking to game design, we agreed on a letter notation (K, M, B, T, AA, AB, AC) which is commonly used in idle games (Gram Games wrote a nice article which we used as inspiration).
IndexToMagnitude =
[
"",
"K",
"M",
"B",
"T"
];
string GetUnit(int magnitude)
{
string unit;
if (magnitude < IndexToMagnitude.Count)
unit = IndexToMagnitude[magnitude];
else
{
var unitInt = magnitude - IndexToMagnitude.Count;
var secondUnit = unitInt % AmountLetters;
var firstUnit = unitInt / AmountLetters;
unit = Convert.ToChar(firstUnit + CharA) +
Convert.ToChar(secondUnit + CharA);
}
return unit;
}
string ToString(IdleNumber idleNumber)
{
return Value.ToString("0.##") + GetUnit();
}
As long as our magnitude (which represents: Exp / 3) is within the predefined list of units, we can just return the unit from the list directly.
ToString(new IdleNumber(1.2345, 3)); > 123K
For numbers bigger than that, we generate the unit which is always 2 digits long by using one modulo operation with the amount of letters in the alphabet to get the first digit and one division operation to get the second unit.
ToString(new IdleNumber(1.2345, 18)); > 123AB
Final thoughts
Finding a solution to our problem required a compromise between speed and precision, a compromise we gladly take. To make sure it works as expected, we wrote lots of unit tests covering all mathematical operations we currently support and the number-formatting, revealing a few issues we had in our initial implementation.

The only real issues that popped afterwards were related to rounding when formatting the number.
The biggest number we can currently display is 999.99ZZ which is a number with 2043 digits – that should last us a while. Do you think we will ever reach this value? What would you do if this limit is reached? Start adding more digits to the unit? Introduce a reset? Ask the game designer what the heck she/he was thinking? 🙂
Cheers!
Sources and more information on that topic:
https://docs.microsoft.com/en-us/office/vba/language/reference/user-interface-help/data-type-summary
https://docs.microsoft.com/en-us/dotnet/api/system.numerics.biginteger?view=netcore-3.1
https://github.com/Osinko/BigFloat
https://stackoverflow.com/questions/17469258/biginteger-performance-for-extremely-large-numbers
https://gamedev.stackexchange.com/questions/114911/how-do-idle-games-handle-such-large-numbers/114916
https://gram.gs/gramlog/formatting-big-numbers-aa-notation/
InnoGames is hiring! Check out open positions and join our awesome international team in Hamburg at the certified Great Place to Work®.